DP问题
之前学过dp,大一上的时候学过一点,现在决定系统性的学遍
线性dp
引入数塔问题
实现
#include<bits/stdc++.h>
using namespace std;
int n;
const int N = 110;
int g[N][N];
int dp[N][N];
int main(){
cin >> n;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cin >> g[i][j];
}
}
for(int i=n-1;i>0;i--){
for(int j=i;j>0;j--){
dp[i][j] = max(dp[i+1][j]+g[i][j],dp[i+1][j+1]+g[i][j]);
}
}
cout << dp[1][1];
return 0;
}
免费馅饼
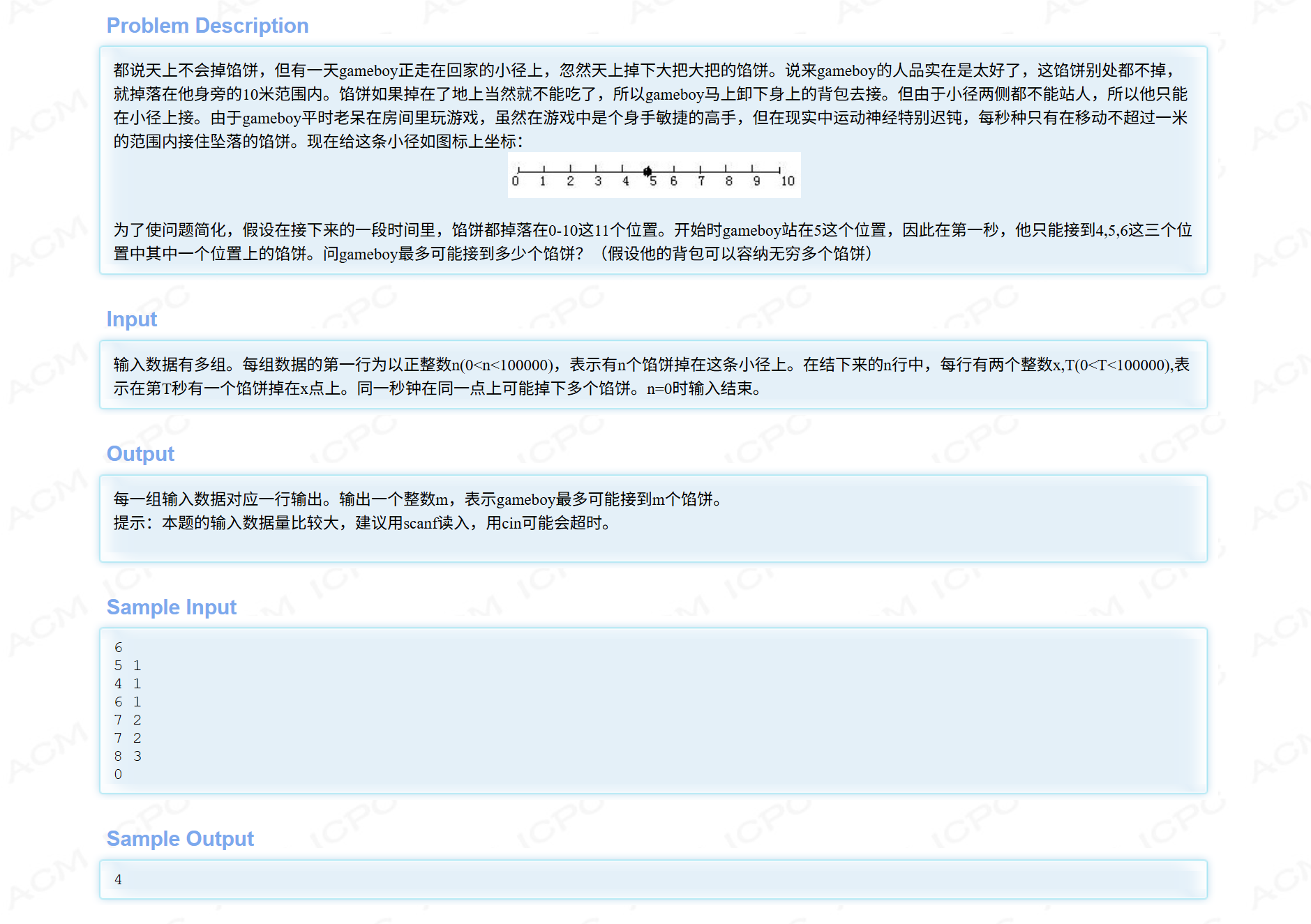
这道题和数塔的题其实差不多,时间从后往前推,寻找路径最大值
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int g[N][11];
int dp[N][11];
int main() {
int n;
while (cin >> n && n != 0) {
memset(g, 0, sizeof(g));
memset(dp, 0, sizeof(dp));
int max_time = 0;
for (int i = 0; i < n; i++) {
int x, T;
scanf("%d %d", &x, &T);
g[T][x]++;
max_time = max(max_time, T);
}
for (int j = 0; j <= 10; j++) {
dp[max_time][j] = g[max_time][j];
}
for (int i = max_time - 1; i >= 1; i--) {
for (int j = 0; j <= 10; j++) {
int current = g[i][j];
if (j == 0) { // j-1越界
dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + current;
} else if (j == 10) {
dp[i][j] = max(dp[i + 1][j - 1], dp[i + 1][j]) + current;
} else {
dp[i][j] = max({dp[i + 1][j - 1], dp[i + 1][j], dp[i + 1][j + 1]}) + current;
}
}
}
// 第一秒只能在4、5、6位置
cout << max({dp[1][4], dp[1][5], dp[1][6]}) << endl;
}
return 0;
}
最长有序子序列
背包dp
01背包
01背包算是动态规划的入门题目 ,对新手来说不是很友好但是也没那么难。

想象dp是一个表格
dp [i] [j] i表示考虑了几种物品,j表示背包的体积
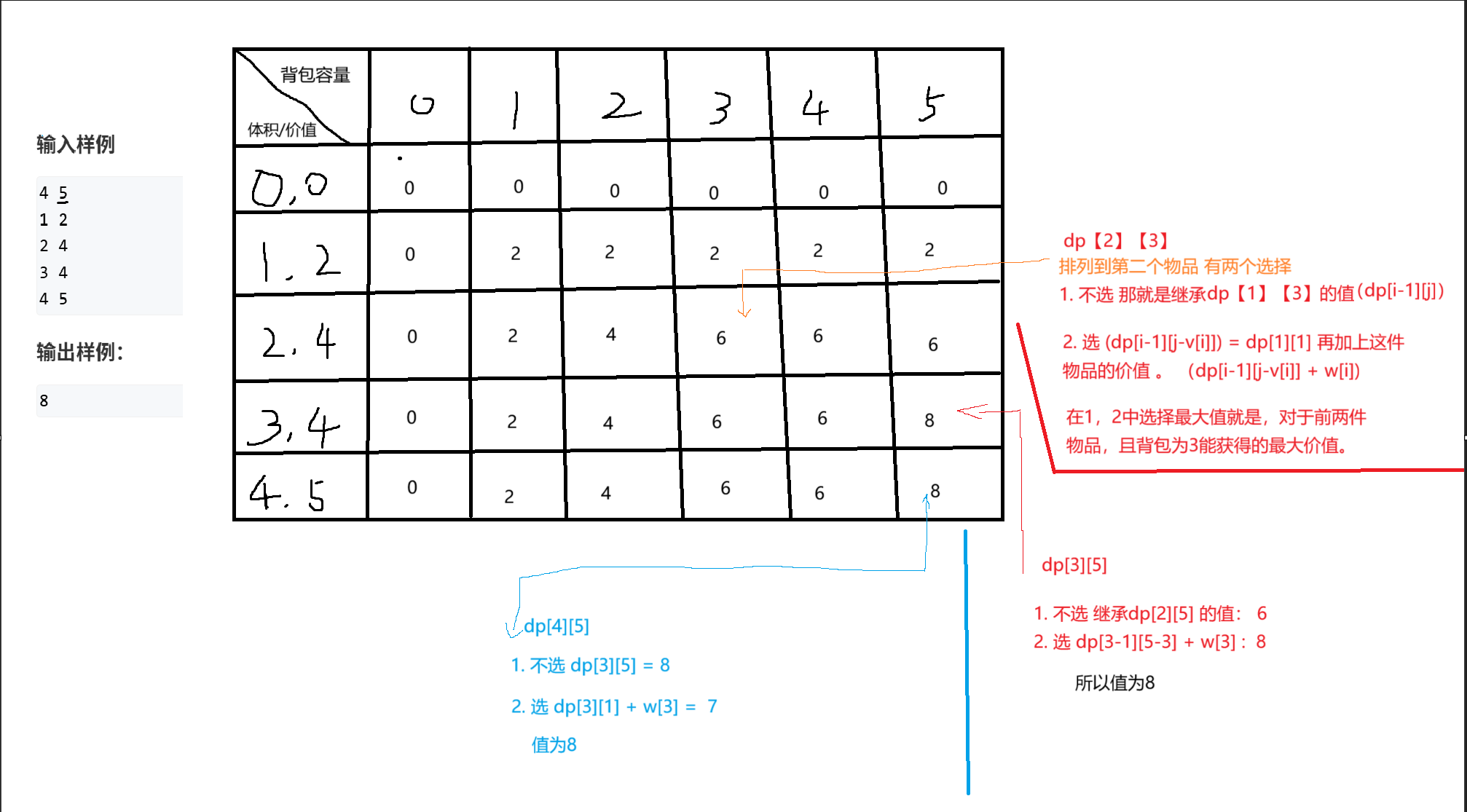
#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N = 1010;
int v[N],w[N];
int dp[N][N];
int main(){
cin >> n >> m;
for(int i=1;i<=n;i++){
cin >> v[i] >> w[i];
}
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
dp[i][j] = dp[i-1][j];
if(j >= v[i]){
dp[i][j] = max(dp[i][j], dp[i-1][j-v[i]]+w[i]);
}
}
}
int ans = INT_MIN;
for(int i=0;i<=m;i++){
ans = max(ans, dp[n][i]);
}
cout << ans;
return 0;
}
01背包还有一维的写法,个人觉得这个二维的更容易理解一些
完全背包
完全背包和01背包差不多 就是多了每个物品可以选无数次

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N = 1010;
int v[N],w[N];
int dp[N][N];
int main(){
cin >> n >> m;
for(int i=1;i<=n;i++){
cin >> v[i] >> w[i];
}
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
dp[i][j] = dp[i-1][j];
if(j >= v[i]){
dp[i][j] = max(dp[i-1][j],dp[i][j-v[i]]+w[i]);
}
}
}
cout << dp[n][m];
return 0;
}
完全背包问题,可以使用闫氏分析法。
主要是状态转移方程,没看过的人可能就是不会做。
正常把完全背包分析完之后的状态转移方程应该是
dp[i][j] = dp[i-1][j];
if(j >= v[i]){
dp[i][j] = max(dp[i][j] , dp[i-1][j-v[i]] + w[i] , dp[i-1][j-2*v[i]] + 2*w[i], ***** ,dp[i-1][j-k*v[i]] + k*w[i]);
}
会发现除了不选以外有很多项,可能会想在加一层for循环,但是再加一层 pow(1000,3)肯定会超时所以,还有别的解决方法
// 可以带入dp[i][j-v]有点像数学方法但是也确实是这样的
dp[i][j-v[i]] = max(dp[i-1][j-v[i]], dp[i-1][j-2*v[i]] + w[i], dp[i-1][j-3*v[i]] + 2*w[i] ,******, dp[i-1][j-k*v[i]] + (k-1)*w[i]);
// 可以发现dp[i][j-v[i]]和dp[i][j]除了第一项不选之外就差一个w【i】 所以完整的状态转移方程就出现了
dp[i][j] = max(dp[i-1][j] , dp[i][j-v[i]] + w[i]);
// 这就是最终的状态转移方程
完全背包dp也有一维的写法
#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N = 1010;
int v[N],w[N];
int dp[N];
int main(){
cin >> n >> m;
for(int i=1;i<=n;i++){
cin >> v[i] >> w[i];
}
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
if(j >= v[i]){
dp[j] = max(dp[j],dp[j-v[i]]+w[i]);
}
}
}
cout << dp[m];
return 0;
}
if 判断可以移动到循环里去,忘记了
区间dp
顾名思义,区间dp就是在区间上进行动态规划,求解一段区间上的最优解;该问题的求解思路主要是通过合并小区间的最优解进而得出整个大区间上最优解的 dp 算法。
就是把一个大区间分化成各种小区间,让后再合并成大区间,有分治的思想 。
石子合并

#include<bits/stdc++.h>
using namespace std;
int n;
const int N = 310;
int s[N];
int f[N][N];
int main(){
cin >> n;
for(int i=1;i<=n;i++){
cin >> s[i];
s[i] += s[i-1];
}
for(int len = 2;len <= n;len ++){ // 设置求的区间长度
for(int i=1;i+len-1 <= n; i++){ // 求i - j 的区间
int j = i + len - 1;
f[i][j] = INT_MAX;
for(int k = i;k < j;k++){
f[i][j] = min(f[i][j], f[i][k] + f[k+1][j] +(s[j] - s[i-1]));
}
}
}
cout << f[1][n];
return 0;
}
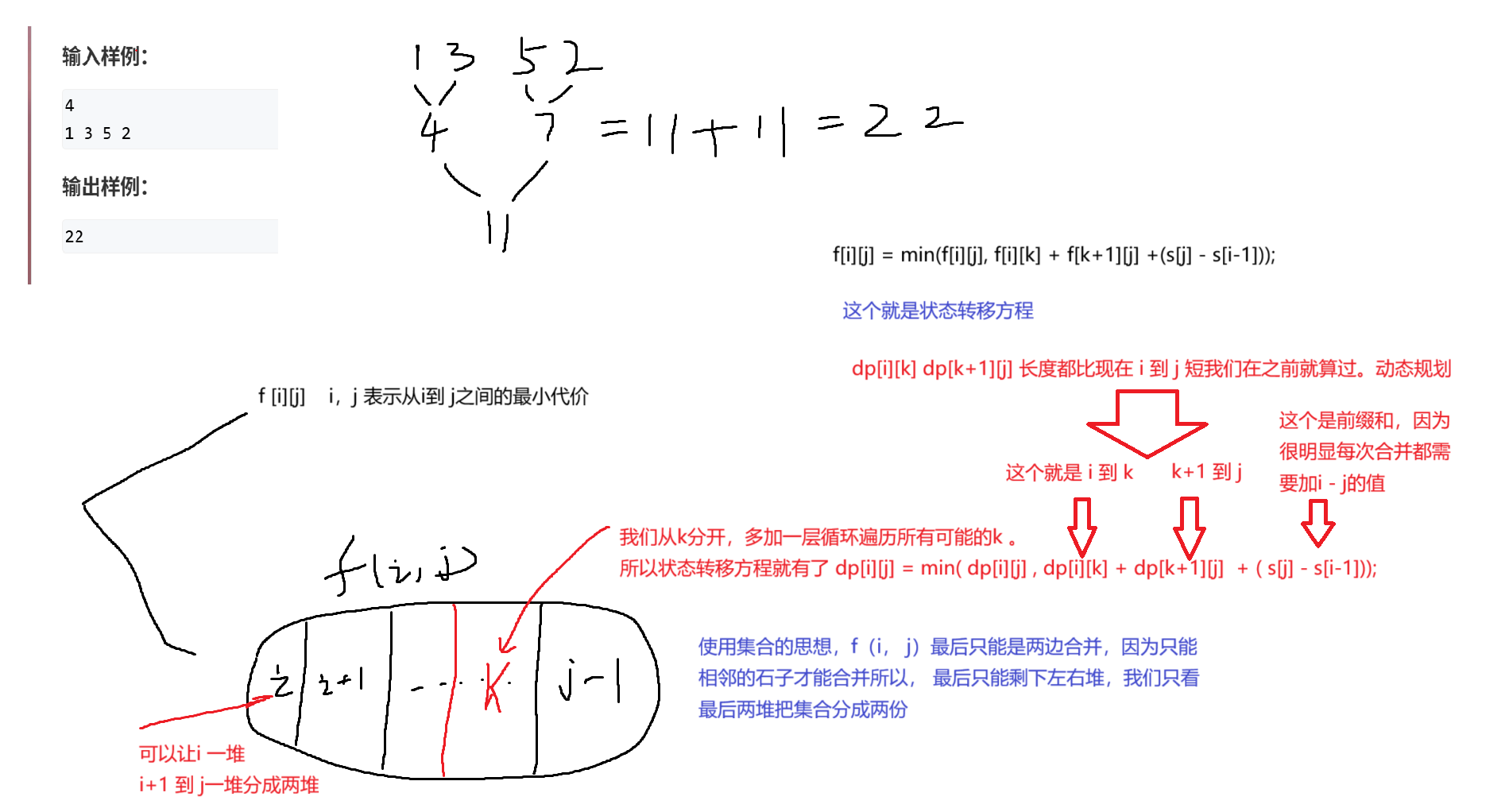
也不是很难,有点像加强版的线性dp


